ACT Math covers a broad range of topics. Some questions test concepts you may have learned in elementary school, such as simple percent questions and adding or subtracting fractions. Other ACT questions test concepts you may not learn in high school at all, such as matrices and vectors.

There is no overall formula sheet provided for the ACT. Some individual questions may provide a formula, but the majority won’t.
The good news is that if you’re thinking about taking the ACT, you probably already have many of these formulas memorized, or can recall them with a quick refresher or two. With the right prep, you might also have other tools and strategies (such as breaking shapes into smaller shapes) that allow you to solve the problem without using a formula. You’ll still need to memorize some formulas, but not as many as you might fear.
How to Study ACT Math Formulas
Prioritize your studies by memorizing formulas in this order:
- Must Know
- Nice to Know (But Can be Solved with Strategy)
- Could Know (But Tested Only Rarely)
As you go through the Must Know formulas below, mark each one as something you:
- Definitely Understand
- Sort of Understand
- Don’t Understand
For the “Definitely Understand” formulas, you’re done-there’s no need to spend any time memorizing formulas you already know. Instead, focus your efforts where you’ll gain the most.
For the “Sort of Understand” and “Don’t Understand” categories, use your favorite memorization strategy: flashcards, apps, writing in a notebook, etc. If you have more than 10 or so formulas to memorize, focus on about 10 at a time.
After mastering the “Must Know” formulas, repeat the same approach with the “Nice to Know” and “Could Know” formulas.
Try to solve some ACT practice questions (or even better, ACT practice tests ) and review your results. This can make it clearer which formula-based questions you’d be able to solve if only you remembered the formula.
Memorization: Consistency is Key
Regardless of your approach, spend some time each day studying your ACT formulas. You’ll see more improvement spending 5-10 minutes a day rather than spending 2 hours once a week cramming.
Geometry Formulas
Most of the formulas you need to memorize for ACT Math are geometry formulas. If you find that you’re missing numerous geometry questions on your homework and practice tests, consider whether your lack of knowledge of the formulas is affecting your score.
Must Know Geometry Formulas
- Area of a Rectangle: A = lw
- Area of a Triangle:
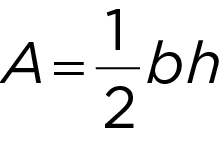
- Area of a Circle: A = π r 2
- Circumference of a Circle: C = π d or C = 2π r
- Diameter and Radius of a circle: d = 2 r
- Volume of a Rectangular Prism: V = Bh , where B is the area of the base
- Degrees in a:
-
Right Angle: 90°
-
Straight Line: 180°
-
Triangle: 180°
-
Circle: 180°
-
- Parallel Lines and Angles – When a line intersects two parallel lines
-
Two kinds of angles are formed: big angles and small angles.
-
Each big angle is equal to the other big angles.
-
Each small angle is equal to the other small angles.
-
Any big angle plus any small angle is 180°.
-
- Pythagorean Theorem: a 2 + b 2 = c 2 , where c is the hypotenuse of a right triangle.
- SOHCAHTOA
Nice to Know (But Can be Solved with Strategy) Geometry Formulas
- Area of a Square: A = s 2 (based on Area of a Rectangle formula)
- Area of a Parallelogram: A = bh (break into 2 triangles or a rectangle and 2 triangles)
- Area of a Trapezoid:
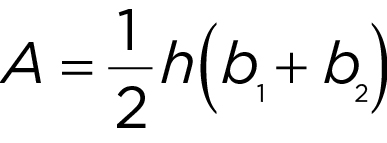 (break into 2 triangles and a rectangle)
(break into 2 triangles and a rectangle) - Volume of a Cube: V = s 3 (based on volume of a rectangular prism)
- Volume of a Rectangular Solid: V = lwh (based on volume of a rectangular prism)
- Volume of a Cylinder: V = π r 2 h (based on volume of a rectangular prism)
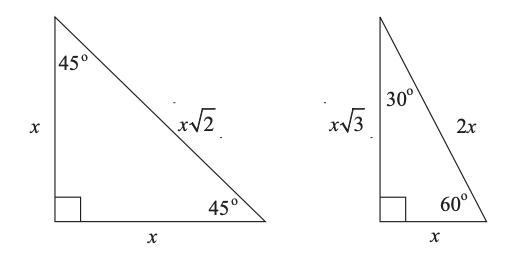
- Special Right Triangles:
(use the Pythagorean theorem)
- Sum of angles in an n -sided polygon: ( n – 2)180° (break polygon into triangles)
- Angle measure of each angle in a regular n -sided polygon:
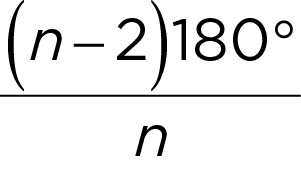 (break polygon into triangles)
(break polygon into triangles) - Surface area of a rectangular solid: S = 2( lw + lh + wh ) (add areas of all faces)
- Surface area of a cube: S = 6 s 2 (add areas of all faces)
- Surface area of a right circular cylinder: S = 2π r 2 + 2π rh (add areas of all faces)
Nice to Know (But Rarely Tested) Geometry Formulas
- Reciprocal Trigonometric Functions:
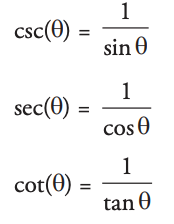
- Law of sines:
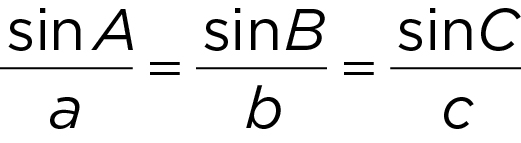
- (sometimes provided in a question)
- Surface area of a sphere: S = 4π r 2 (sometimes provided in a question)
- Volume of a sphere:
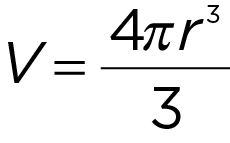 (sometimes provided in a question)
(sometimes provided in a question)
Coordinate Geometry Formulas
Some ACT Coordinate Geometry questions are really just geometry questions in disguise, but other questions will require formulas specific to this area of study.
Must Know Coordinate Geometry Formulas
- Slope:
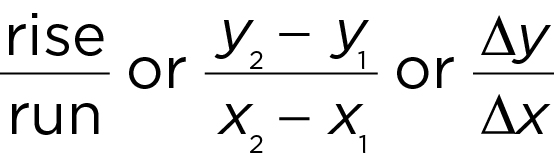
- Slope-intercept form of a line: y = mx + b , where m is the slope and b is the y -intercept
Nice to Know (But Can be Solved with Strategy) Coordinate Geometry Formulas
- Distance:
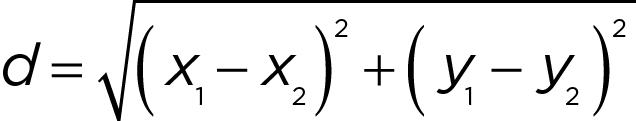 (make the distance the hypotenuse of a right triangle and use the Pythagorean theorem)
(make the distance the hypotenuse of a right triangle and use the Pythagorean theorem) - Midpoint:
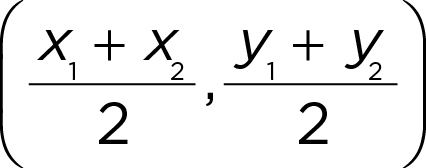 (the average of the x -coordinates is the midpoint’s x ; same with the y -coordinates)
(the average of the x -coordinates is the midpoint’s x ; same with the y -coordinates) - Standard form: Ax + By = C (can always rearrange into slope-intercept form)
-
Slope:
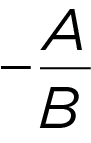
-
y -intercept:
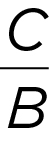
-
Nice to Know (But Rarely Tested) Coordinate Geometry Formulas
- Circle centered at (0,0) = x 2 + y 2 = r 2 , where r is the radius
- Circle centered at ( h , k ) = ( x – h ) 2 + ( y – k ) 2 = r 2 , where r is the radius

(sometimes given in a question)
Algebra Formulas
There are a couple of formulas that are useful when specifically working with quadratics in the form ax 2 + bx + c = 0:
Quadratic formula:
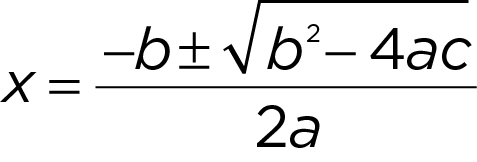
Discriminant: D = b 2 – 4 ac (the expression under the radical in the quadratic formula)
- If D > 0, there will be two distinct, real solutions.
- If D = 0, there will be one distinct real solution.
- If D < 0, there will be no real solutions. Instead, there will be two complex solutions.
The sum of the roots:
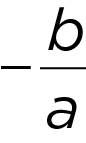
The product of the roots:

The midpoint of the roots/the
x -coordinate of the vertex:
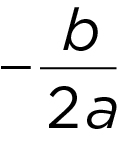
Problem Solving Formulas
Most questions testing the following formulas can be solved with careful reading and strategy. However, if you’re the sort that prefers to memorize, these can be helpful to know.
- Arithmetic sequence: n th term = Original Term + ( n – 1) d , where d is the constant difference between terms
- Direct Variation:
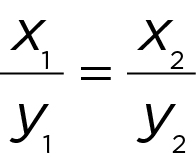 or y = kx , where k is a constant
or y = kx , where k is a constant - Inverse Variation: x 1 y 1 = x 2 y 2 or
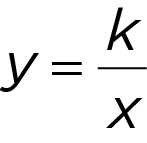 , where k is a constant
, where k is a constant - Geometric sequence: n th term = Original Term ´ r ( n – 1) , where r is the constant ratio between terms
- Group Formula: Total = Group 1 + Group 2 – Both + Neither
Statistics Formulas
Most ACT Math statistics questions will test basic formulas that you learned in middle school. However, there may be a few questions testing some more advanced statistics concepts.
- Average (Arithmetic Mean) = Total = Average ´ Number of Things
- Probability: ">
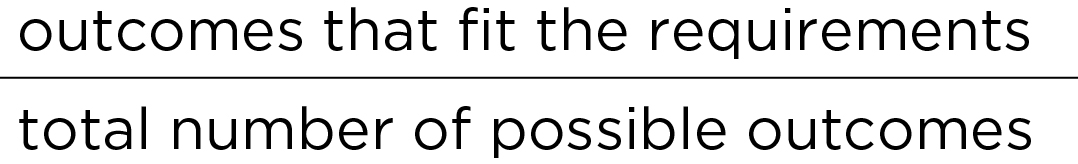
- Permutations (the number of ways to arrange or order a group of things):
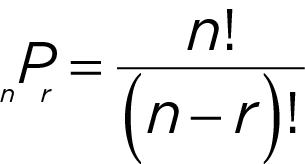
- n P r = , where n is the number of elements available and r is the number of elements chosen
- Combinations (the number of ways make different groups out of a group of things):
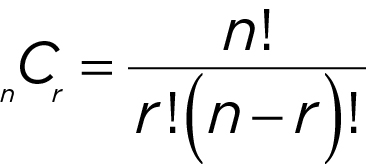
- n C r = , where n is the number of elements available and r is the number of elements chosen.
- Expected value: Multiply the probability of each occurrence by the value of that occurrence, then add the sums.
Knowing the ACT math formulas can be very helpful when taking your exam. However, the bigger challenge is learning effective strategies to answer questions correctly and quickly. The Princeton Review offers books, courses, and tutoring to help you learn the approaches needed to beat ACT Math and earn the score of your dreams.
Explore Colleges For You
Connect with our featured colleges to find schools that both match your interests and are looking for students like you.
Get Started on Athletic Scholarships & Recruiting!
Join athletes who were discovered, recruited & often received scholarships after connecting with NCSA's 42,000 strong network of coaches.
Best 390 Colleges
168,000 students rate everything from their professors to their campus social scene.
Explore Colleges For You
Connect with our featured colleges to find schools that both match your interests and are looking for students like you.
Get Started on Athletic Scholarships & Recruiting!
Join athletes who were discovered, recruited & often received scholarships after connecting with NCSA's 42,000 strong network of coaches.
Best 390 Colleges
168,000 students rate everything from their professors to their campus social scene.
Explore Colleges For You
Connect with our featured colleges to find schools that both match your interests and are looking for students like you.
Get Started on Athletic Scholarships & Recruiting!
Join athletes who were discovered, recruited & often received scholarships after connecting with NCSA's 42,000 strong network of coaches.
Best 390 Colleges
168,000 students rate everything from their professors to their campus social scene.